PSO_SVM分类测试及分类结果可视化

发表于 分类于 ， ， 阅读次数： 本文字数： 4.6k 阅读时长 ≈ 4 分钟

训练集wine：

Snipaste_2024-05-06_19-49-26.png

Snipaste_2024-05-06_19-50-54.png

训练集的可视化：

Snipaste_2024-05-06_19-56-54.png

PSO-SVM运行代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
%%
clc
clear all
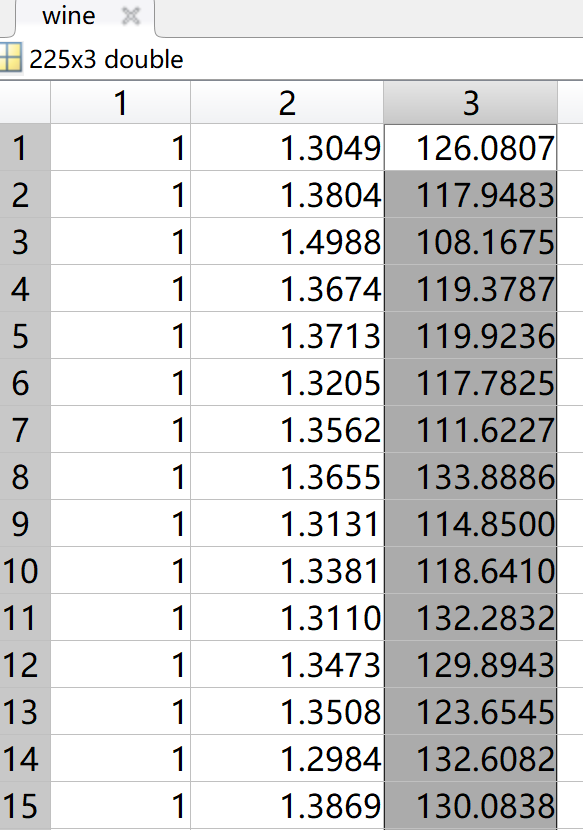
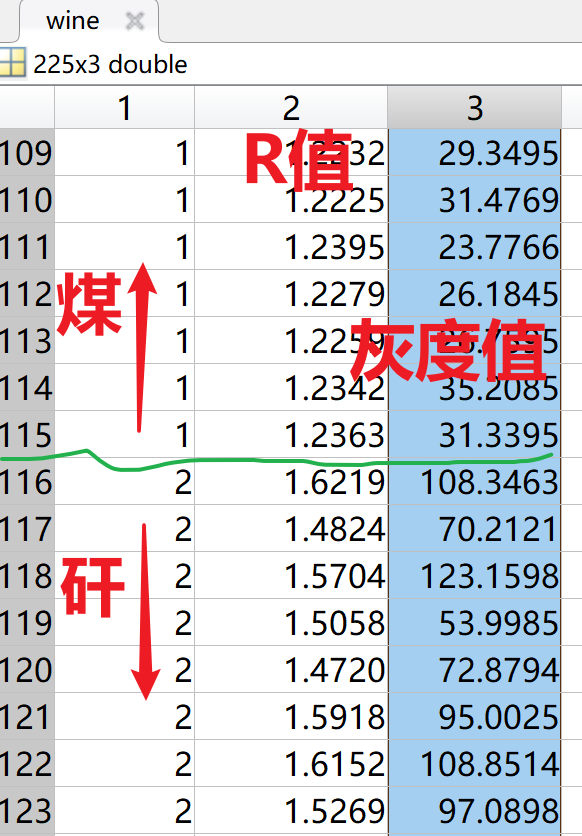
load wine.mat;
data1 = wine(1:115,:);
data2 = wine(116:225,:);
%选择两维进行分类可视化
p = 2;
q = p+1;
%合并样本数据
data0=[data1;data2];
train_data=data0(:,p:q);
train_label=data0(:,1);
%将选定训练集进行归一化
[train_data,pstrain] = mapminmax(train_data');
pstrain.ymin = 0;
pstrain.ymax = 1;
[train_data,pstrain] = mapminmax(train_data,pstrain);
train_data =train_data';


%原始样本分布图灰度均值与灰度方差
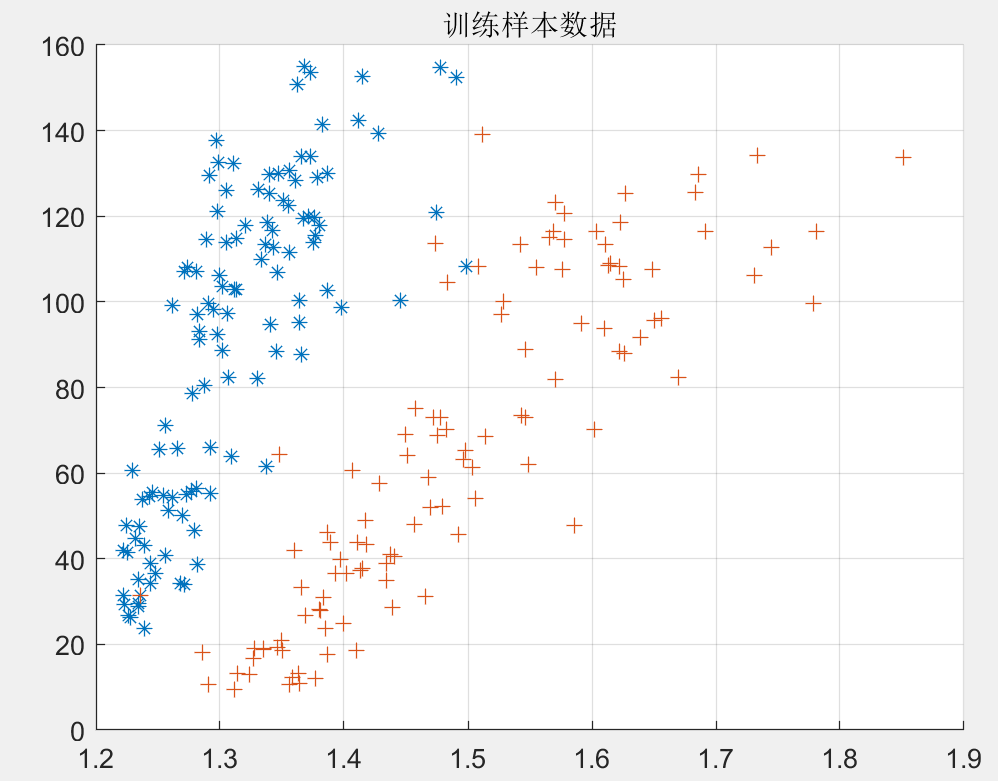
figure('NumberTitle', 'on', 'Name','灰度均值与灰度方差');
hold on;
grid on;
plot(data1(:,p),data1(:,q),'*'),
plot(data2(:,p),data2(:,q),'+'),
title('训练样本数据');
%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.6; % c1 belongs to [0,2]
c2 = 1.5; % c2 belongs to [0,2]
maxgen=200;   % 进化次数 
sizepop=30;   % 种群规模
popcmax=10^(2);
popcmin=10^(-1);
popgmax=10^(3);
popgmin=10^(-2);
k = 0.6; % k belongs to [0.1,1.0];
Vcmax = k*popcmax;
Vcmin = -Vcmax ;
Vgmax = k*popgmax;
Vgmin = -Vgmax ;
% SVM参数初始化,随机的将数据分为3个部分
v = 3;
%% 产生初始粒子和速度
for i=1:sizepop
    % 随机产生种群
    pop(i,1) = (popcmax-popcmin)*rand+popcmin;    % 初始种群
    pop(i,2) = (popgmax-popgmin)*rand+popgmin;
    V(i,1)=Vcmax*rands(1);  % 初始化速度
    V(i,2)=Vgmax*rands(1);
    % 计算初始适应度
    cmd = ['-v ',num2str(v),' -c ',num2str( pop(i,1) ),' -g ',num2str( pop(i,2) )];
    fitness(i) = libsvmtrain(train_label,train_data, cmd);
    fitness(i) = -fitness(i);
end
% 找极值和极值点
[global_fitness,bestindex]=min(fitness); % 全局极值
local_fitness=fitness;   % 个体极值初始化
global_x=pop(bestindex,:);   % 全局极值点
local_x=pop;    % 个体极值点初始化
tic
%% 迭代寻优
for i=1:maxgen
   
    for j=1:sizepop
       
        %速度更新
        wV = 0.9; % wV best belongs to [0.8,1.2]
        V(j,:) = wV*V(j,:) + c1*rand*(local_x(j,:) - pop(j,:)) + c2*rand*(global_x - pop(j,:));
        if V(j,1) > Vcmax
            V(j,1) = Vcmax;
        end
        if V(j,1) < Vcmin
            V(j,1) = Vcmin;
        end
        if V(j,2) > Vgmax
            V(j,2) = Vgmax;
        end
        if V(j,2) < Vgmin
            V(j,2) = Vgmin;
        end
       
        %种群更新
        wP = 0.6;
        pop(j,:)=pop(j,:)+wP*V(j,:);
        if pop(j,1) > popcmax
            pop(j,1) = popcmax;
        end
        if pop(j,1) < popcmin
            pop(j,1) = popcmin;
        end
        if pop(j,2) > popgmax
            pop(j,2) = popgmax;
        end
        if pop(j,2) < popgmin
            pop(j,2) = popgmin;
        end
       
        % 自适应粒子变异
        if rand>0.5
            k=ceil(2*rand);
            if k == 1
                pop(j,k) = (20-1)*rand+1;
            end
            if k == 2
                pop(j,k) = (popgmax-popgmin)*rand+popgmin;
            end           
        end
       
        %适应度值
        cmd = ['-v ',num2str(v),' -c ',num2str( pop(j,1) ),' -g ',num2str( pop(j,2) )];
        fitness(j) = libsvmtrain(train_label,train_data, cmd);
        fitness(j) = -fitness(j);
    end
   
    %个体最优更新
    if fitness(j) < local_fitness(j)
        local_x(j,:) = pop(j,:);
        local_fitness(j) = fitness(j);
    end
   
    %群体最优更新
    if fitness(j) < global_fitness
        global_x = pop(j,:);
        global_fitness = fitness(j);
    end
   
    fit_gen(i)=global_fitness;   
       
end
toc
%% 结果分析
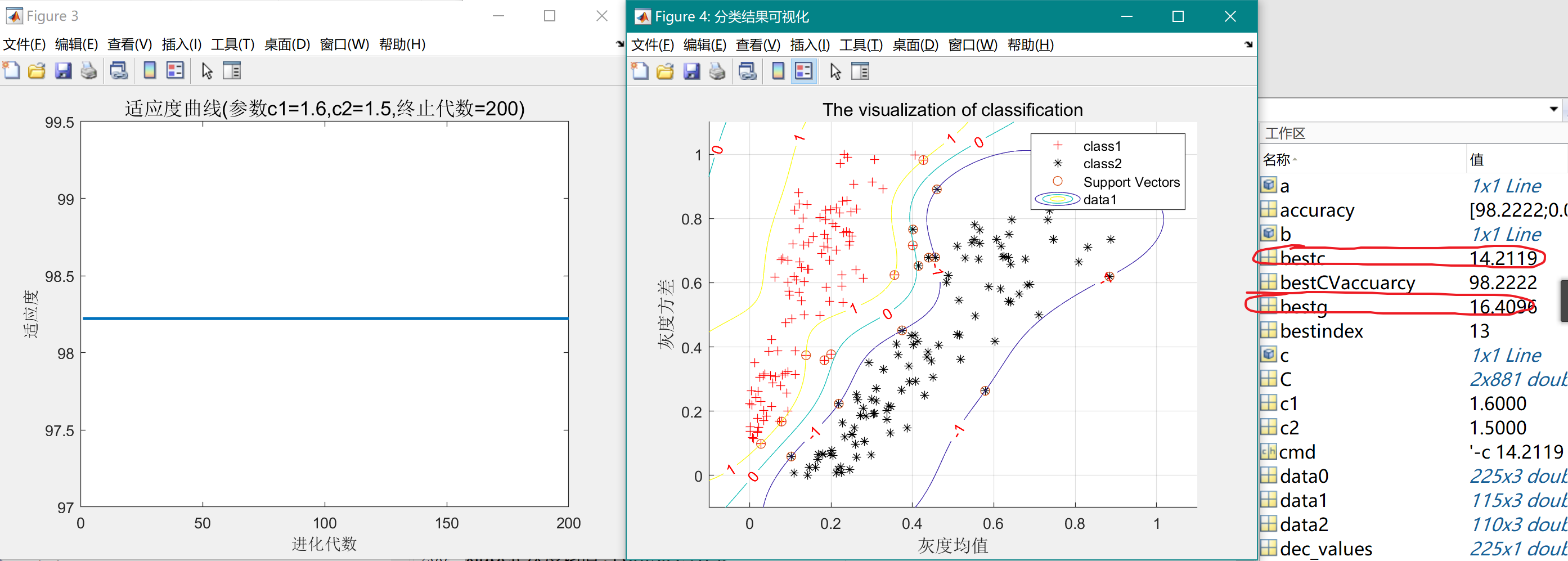
figure,
plot(-fit_gen,'LineWidth',2);
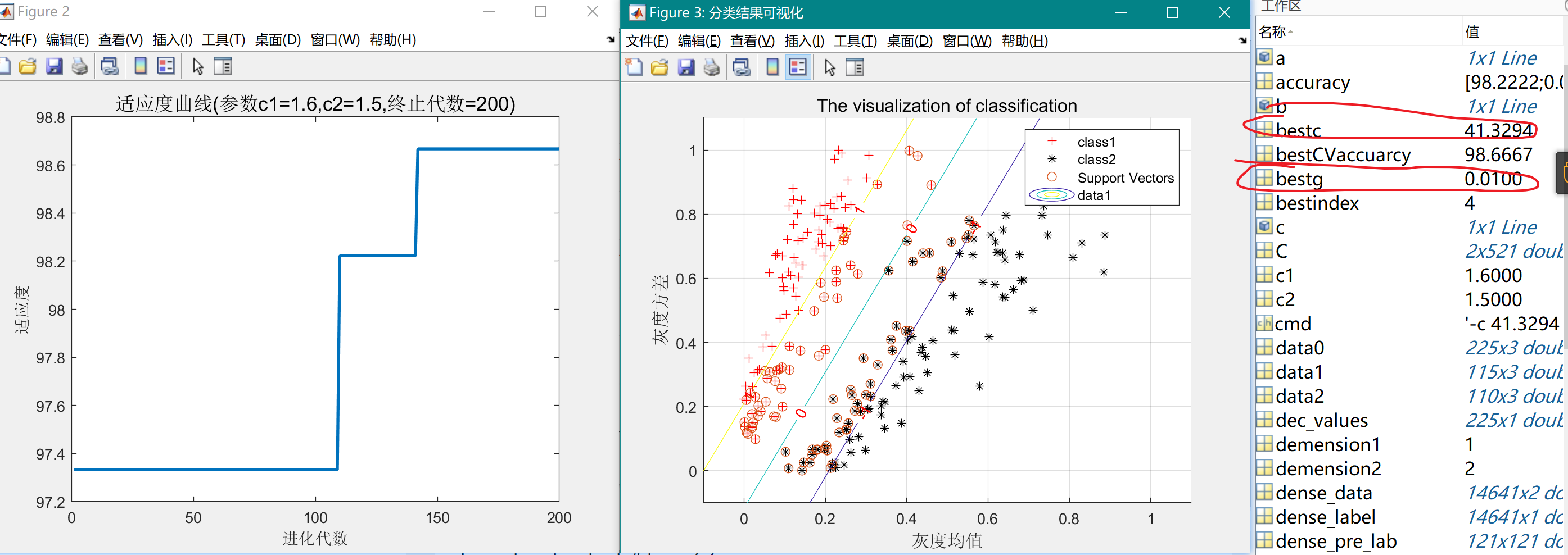
title(['适应度曲线','(参数c1=',num2str(c1),',c2=',num2str(c2),',终止代数=',num2str(maxgen),')'],'FontSize',13);
xlabel('进化代数');ylabel('适应度');
bestc = global_x(1)
bestg = global_x(2)
bestCVaccuarcy = -fit_gen(maxgen);
cmd = ['-c ',num2str( bestc ),' -g ',num2str( bestg )];

分类结果可视化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
model=libsvmtrain(train_label,train_data,cmd); %径向基函数
test_label=train_label;
test_data=train_data;
[predict_label,accuracy,dec_values] = svmpredict(test_label,test_data, model);

%%
demension1 = 1;
demension2 = 2;
minX = min(test_data(:, demension1));
maxX = max(test_data(:, demension1));
minY = min(test_data(:, demension2));
maxY = max(test_data(:, demension2));

gridX = (maxX - minX) ./ 100;
gridY = (maxY - minY) ./ 100;

minX = minX - 10 * gridX;
maxX = maxX + 10 * gridX;
minY = minY - 10 * gridY;
maxY = maxY + 10 * gridY;

[denseX, denseY] = meshgrid(minX:gridX:maxX, minY:gridY:maxY);

%%

model.Parameters(1) = 3; 
[m,n]=size(denseX);
dense_data=[reshape(denseX,m*n, 1), reshape(denseY,m*n,1)];
dense_label = ones(m*n,1);
%密集点分类
model.Parameters(1) = 3;
[lab] =svmpredict(dense_label,dense_data, model);
dense_pre_lab = reshape(lab, m,n);

%%
%画分类后的点及SV
figure('NumberTitle', 'on', 'Name','分类结果可视化');
hold on;
grid on;
m=length(predict_label);
for i=1:m
    if (predict_label(i)==1)
    a= plot(test_data(i, 1), test_data(i, 2), 'r+');    
    end
    if (predict_label(i)==2)
      b= plot(test_data(i, 1), test_data(i, 2), 'k*');  
    end
end
c= plot( model.SVs(:,1),model.SVs(:,2),'o' );
legend([a,b,c],'class1','class2','Support Vectors');

[C,h] = contour(denseX, denseY, dense_pre_lab,-1:1);
clabel(C,h,'Color','r');
xlabel('灰度均值','FontSize',12);
ylabel('灰度方差','FontSize',12);
title('The visualization of classification','FontSize',12);

输出适应度曲线及分类结果可视化：

Snipaste_2024-05-06_20-23-54.png

Snipaste_2024-05-06_19-52-09.png