煤矸双能X射线透射图像余辉校正

发表于 更新于 分类于 ， 阅读次数： 本文字数： 12k 阅读时长 ≈ 10 分钟

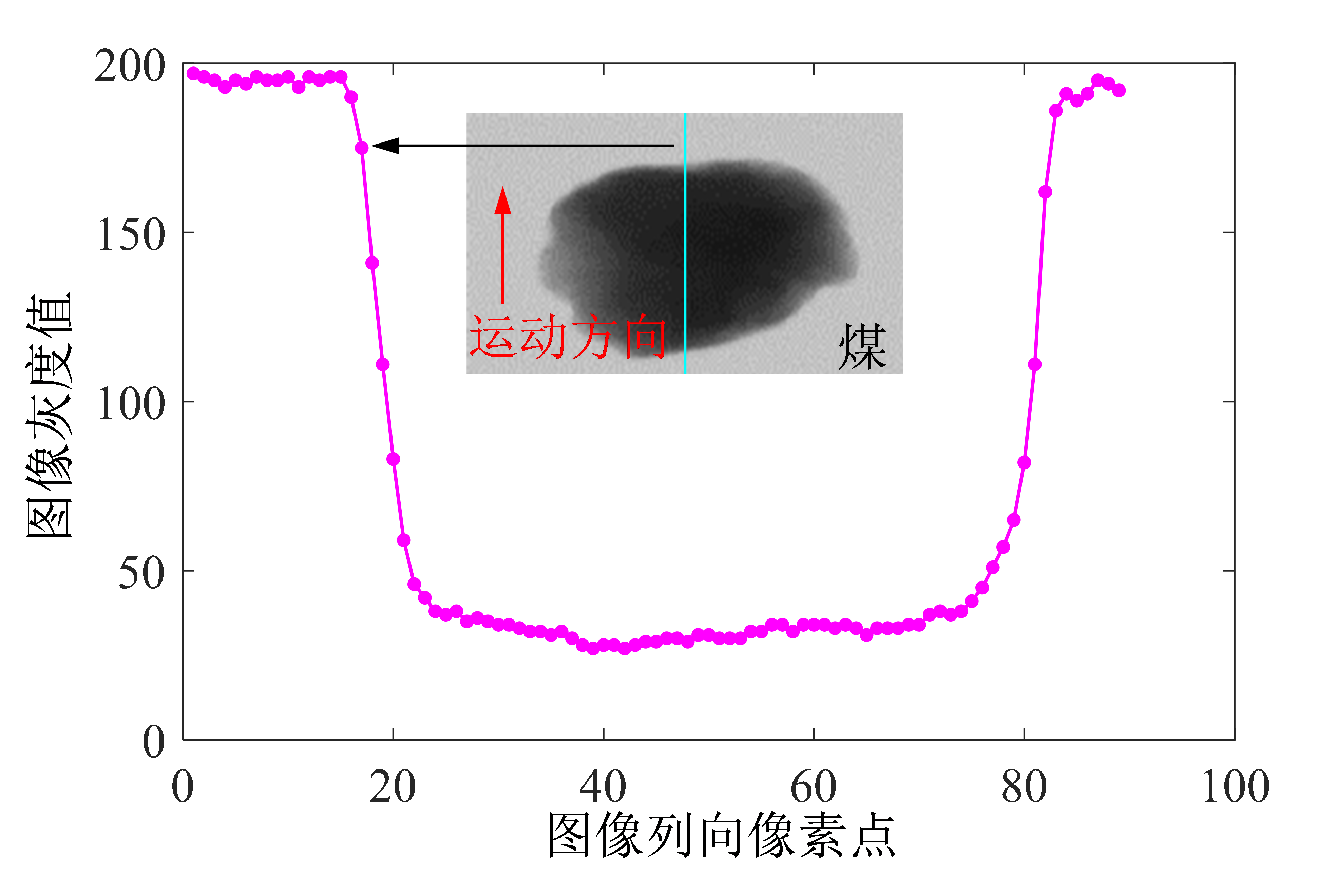
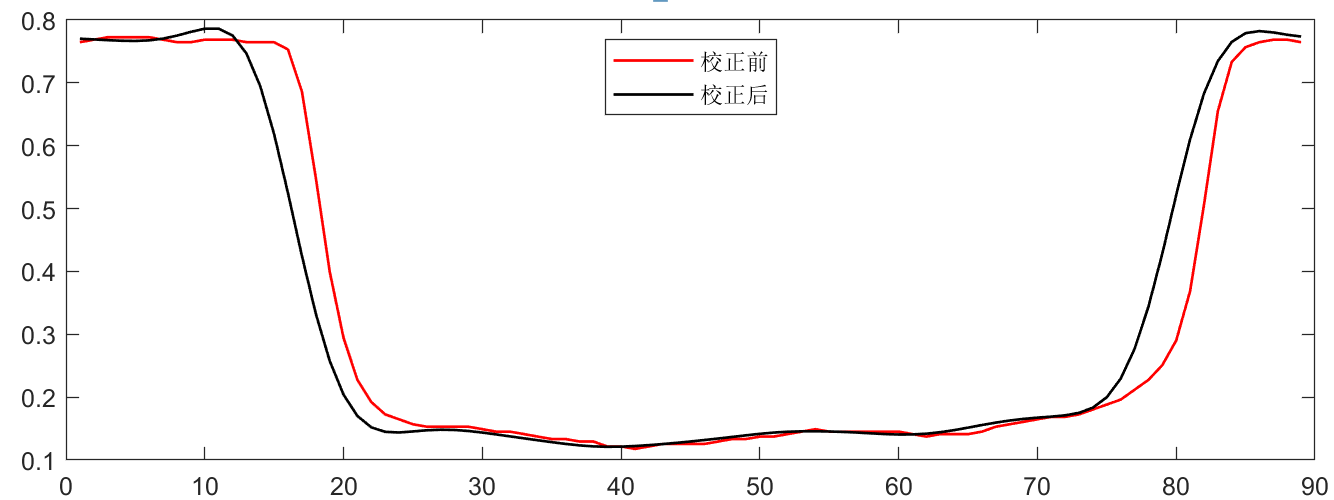
余辉效应又称余辉“拖尾”，是由X射线探测器闪烁体延时和采集电路的积分效应共同导致的。闪烁体余辉近似按指数函数衰减，由“拖尾”引起的图像模糊可以看作是一种线性位置不变的退化过程。实际上，煤矸在皮带上经过运送接受X射线扫描，穿透煤矸的X射线需经过闪烁体或积分计算才能显示输出图像，此延时致使采集的X射线图像存在一定的伪影和模糊现象。煤的余辉效应现象如下图 所示，沿煤的运动方向选取一列像素，X射线穿透煤在图像上表现为灰度值的下降。若无余辉效应则灰度值应从背景值快速下降，而实际成像过程中灰度值呈现缓慢下降。但需要注意的是灰度值并非垂直下降，因为煤一般周向厚度薄。

1.png

消除煤矸DE-XRT厚度和射束硬化效应的根本方法是对X射线自身进行改变，获取具有单一能量的X射线束。实现单一能量X射线获取难度极大，避而求之可采用以下三种方式：选择激发、选择滤光和选择探测。选择激发通过改变X射线产生方式避开韧致辐射，直接获得大量的单一能量的特征辐射。选择探测则要求探测器具有能量分辨能力，目前光子计数型探测器可以实现多能量X射线探测。选择滤光是在X射线在穿透煤矸前把能量不一的X射线束初步滤除至一个较窄范围能量区间。选择激发难度较大，光子计数型探测器成本较高，目前可行的便是选择滤光。选择滤光包括金属滤光和平行滤光两种方法，其中平行滤光优于金属滤光的效果，对物质属性R值的计算精度更高。然而应用平行、金属滤光最终计算的物质属性R值误差仍然随厚度和密度的增加不断增加。因此不再深入讨论对煤矸DE-XRT厚度和射束硬化效应的复原。

煤矸DE-XRT图像高速采集过程中余辉效应将影响后续的识别和定位。常用余辉复原方法有逆滤波和维纳滤波等， 其中逆滤波在目前的安检系统中较为常用。在本研究中主要对比分析逆滤波、维纳滤波、Lucy-Richardson、约束最小二乘复原四种方法的校正效果。

点扩散函数

采集厚铅板DE-XRT透射图像，由于铅板厚度X射线无法穿透，其成像边缘应当从背景值迅速下降至本底值，然而实际上的边缘像素值呈缓慢下降趋势。点扩散函数PSF从开始下降的像素值获取，连续取8列数据至本底值，对点扩散函数PSF进行归一化处理：

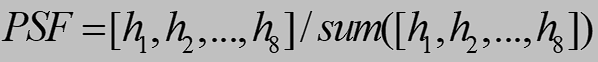
Snipaste_2024-04-14_20-12-13.png

2.png

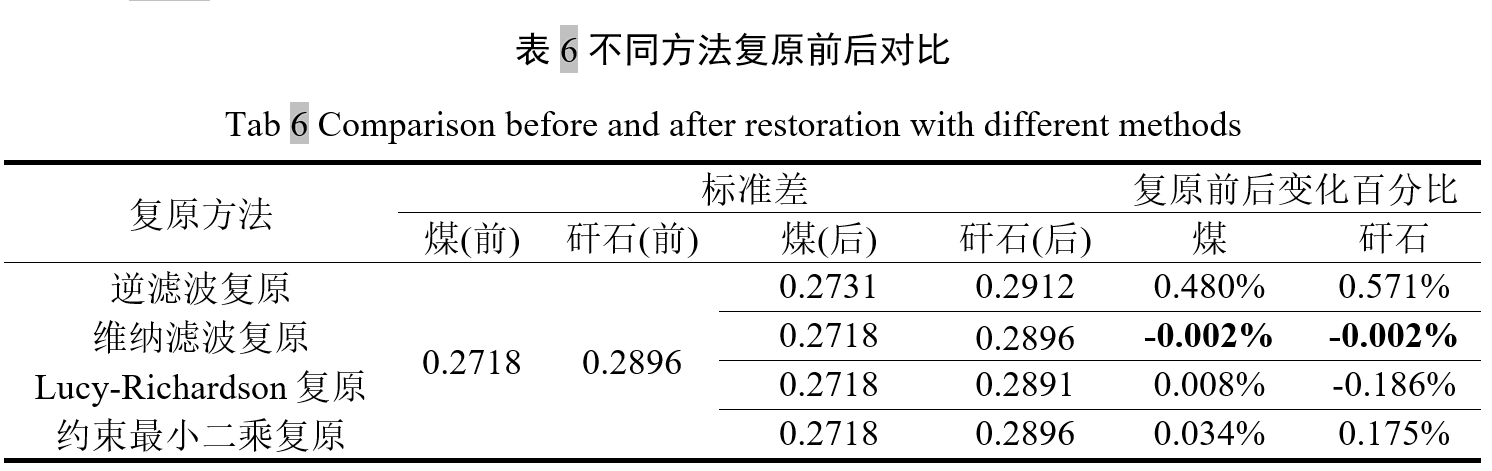
对均匀背景图像进行余辉复原，以复原前后的图像标准差为评价标准，对比分析不同方法的最终复原结果。在MATLAB中维纳滤波、Lucy-Richardson以及约束最小二乘复原均需要预设参数，由于原图像无法获取，因此难以确定具体的参数设定。经多次测试维纳滤波参数SNR设定值为0.005；Lucy-Richardson选择5次迭代，参数WEIGHT为1矩阵，大小与图像相同，DAMPAR偏差阈值设定为sqrt(V=0.1)；约束最小二乘参数噪声强度NOISEPOWRE设定为2。以此参数设定复原后图像方差相对复原前方差最小，结果如下表 所示。

Snipaste_2024-04-14_20-32-17.png

逆滤波

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
clear all;
close all;
I = imread('C:\Users\雷子\Desktop\桌面文件\图像校正复原\余辉效应\2.bmp');
load PSF.mat;
I = I(:,:,1);
% I = I(1:1000,50:1000);
I = im2double(I);
% I = rgb2gray(I);
% I = im2double(I);
PSF= PSF./ sum(PSF);
W = fspecial('gaussian',[3,3],0.8);
I = imfilter(I , W, 'replicate');   

%逆滤波
F = edgetaper(I,PSF');
subplot(121), imshow(I);
subplot(122), imshow(F);
[J,P]=deconvblind(F,PSF');

%
figure;
subplot(121), imshow(I);
subplot(122), imshow(J);
plot(I(:,80),'r'), hold on;
plot(J(:,80),'k'), hold on;

矸石逆滤波复原前后：

Snipaste_2024-04-14_20-13-36.png

查看其列向像素变化：

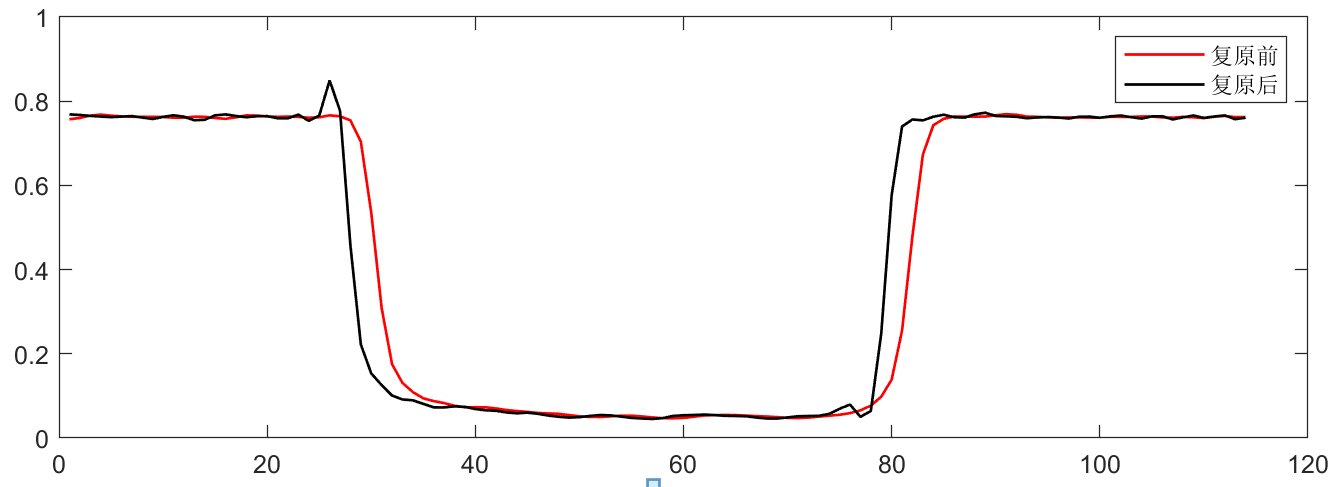
Snipaste_2024-04-14_20-16-25.png

可以看到经过滤波后，目标边缘像素值有突变，还要对其进行消除：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
%对校正进行修复
[m,n] = size(J);
for  i = 1:m
    for j = 1:n
        if J(i,j) >=0.8
            J(i,j) = 0.76;
        end
    end
end

for  i = 1:m
    for j = 1:n
        if J(i,j) <=0.02
           J(i,j) = 0.047;
        end
    end
end
%滤波处理
% W = fspecial('gaussian',[3,3],0.8);
% J= imfilter(J, W, 'replicate');   

figure;
subplot(121), imshow(I);
subplot(122), imshow(J);
plot(I(:,80),'r'), hold on;
plot(J(:,80),'k'), hold on;

对校正进行修复后：

Snipaste_2024-04-14_20-18-21.png

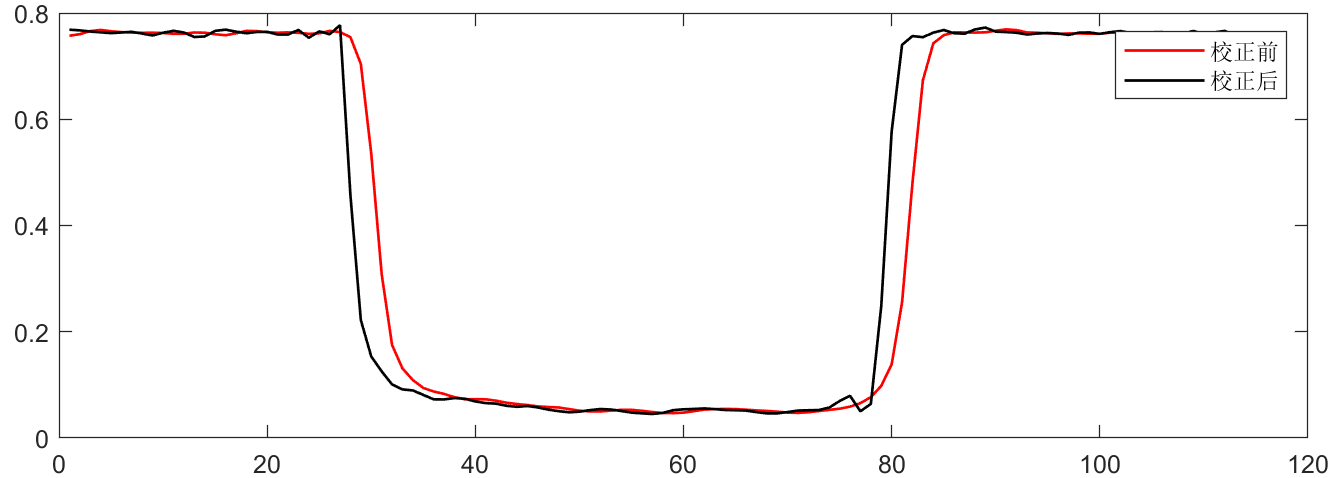
Snipaste_2024-04-14_20-18-56.png

经过校正修复后，图像边缘白色区域较少，像素点不会发生突变。滤波前后，矸石的下边缘明显变黑。

校正会使得像素点下降速度增加，同时采用维纳滤波也会使得平台区域像素点发生变化。

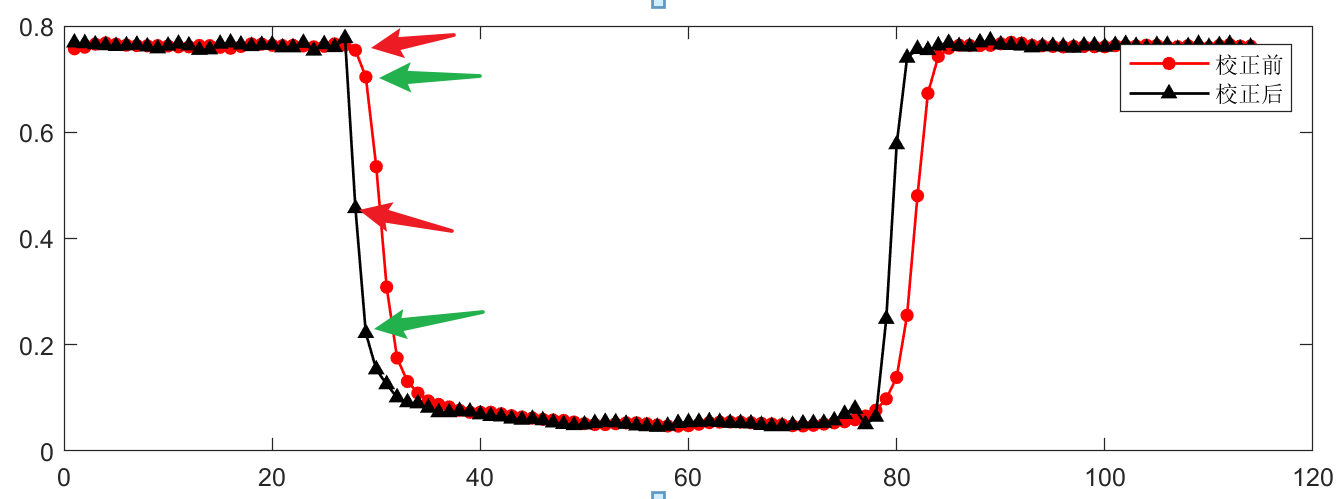
Snipaste_2024-04-14_20-23-36.png

接下来是对一些参数的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
%校正前后参数变化
%图像的灰度均值
ME1 = mean(mean(I));
ME2 = mean(mean(J));

%计算评价参数均方根误差RMSE
for i= 1:m
    for j = 1:n
        S(i,j) =double((J(i,j)-double(I(i,j)))^2);
    end
end
RSME  =( (sum(sum(S))/(m*n)))^(1/2);
%峰值信噪比PSNR
PSNR = 10*log10(255^2/RSME);

%方差与不均匀度
for i = 1:m
        for j = 1:n
             STD1(i,j)= double((double(I(i,j))-ME1)^2);
        end
end
STD = (sum(sum(STD1))/(m*n))^(1/2);
DET1 = STD/ME1;

for i = 1:m
        for j = 1:n
             STD2(i,j)= double((double(J(i,j))-ME2)^2);
        end
end
STD3 = (sum(sum(STD2))/(m*n))^(1/2);
DET2 = STD3/ME2;

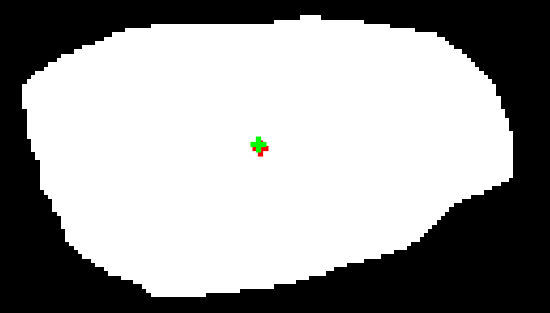
校正前后，采用OTSU阈值分割，目标的形心位置将发生改变：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
%质心位置
thersh_H1 = graythresh(I);
im_bw1 = im2bw(I,thersh_H1);
figure,imshow(im_bw1);
thersh_H2 = graythresh(J);
im_bw2 = im2bw(J,thersh_H2);
figure,imshow(im_bw2);

% BW3 = I.*im_bw1;
% figure,imshow(BW3);
%二值化取反
im_bw1 = ~im_bw1;
im_bw2 = ~im_bw2;
%标注二进制图像中已连接的部分
[L,num]=bwlabel(im_bw1,8);     
[L1,num1]=bwlabel(im_bw2,8);     
%封装函数获取各种参数信息
stats_1 = regionprops(L,'Area','PixelList','Centroid','BoundingBox');
stats_2 = regionprops(L1,'Area','PixelList','Centroid','BoundingBox');
%绘制质心坐标
Cen_1 = cat(1,stats_1.Centroid);
Cen_2 = cat(1,stats_2.Centroid);
figure(8),imshow(im_bw1);
hold on ;
for i=1:length(stats_1) 
    plot(Cen_1(i,1), Cen_1(i,2), 'r+'); 
end
for i=1:length(stats_1) 
    plot(Cen_2(i,1), Cen_2(i,2), 'g+'); 
end
%绘制最小外接矩形框
Temp_1 = cat(1,stats_1.BoundingBox);
for i=1:length(stats_1) 
    temp = Temp_1(i,:);
    rectangle('position',temp,'edgecolor','r');
end 
%标记外接矩形框起始点坐标
for i = 1:length(stats_1)
    plot(Temp_1(i,1),Temp_1(i,2),'g+');
    text(stats_1(i).BoundingBox(1)-10,stats_1(i).BoundingBox(2),num2str(i),'Color','y','FontSize',12);
end
hold on;
%

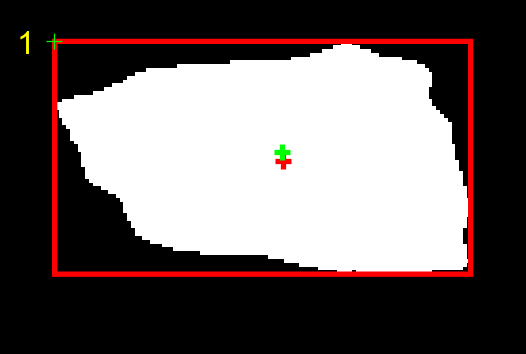
Snipaste_2024-04-14_20-28-50.png

从上图可以看到，校正前目标形心位置是红色，校正后再采用OTSU阈值分割形心位置是绿色，在列向发生了一定的偏移。

维纳滤波

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
clear all;
close all;
I = imread('C:\Users\雷子\Desktop\桌面文件\图像校正复原\余辉效应\1.bmp');
load PSF.mat;
W = fspecial('gaussian',[3,3],0.8);
I = imfilter(I , W, 'replicate');   

I = I(:,:,1);
I = im2double(I);
%维纳滤波
% I = edgetaper(I,PSF');
PSF= PSF./ sum(PSF);
NSR=0.005;
J=deconvwnr(I,PSF',NSR);
%
% J = J.*605;
figure;
subplot(121), imshow(I);
subplot(122), imshow(J);

plot(I(:,70),'r'), hold on;
plot(J(:,70),'k'), hold on;
%对校正进行修复
[m,n] = size(J);
for  i = 1:m
    for j = 1:n
        if J(i,j) >=0.8
            J(i,j) = 0.74;
        end
    end
end

for  i = 1:m
    for j = 1:n
        if J(i,j) <=0.02
           J(i,j) = 0.047;
        end
    end
end
%滤波处理
W = fspecial('gaussian',[3,3],0.8);
J= imfilter(J, W, 'replicate');   

figure;
subplot(121), imshow(I);
subplot(122), imshow(J);
plot(I(:,80),'r'), hold on;
plot(J(:,80),'k'), hold on;

%校正前后参数变化
%图像的灰度均值
ME1 = mean(mean(I));
ME2 = mean(mean(J));

%计算评价参数均方根误差RMSE
for i= 1:m
    for j = 1:n
        S(i,j) =double((J(i,j)-double(I(i,j)))^2);
    end
end
RSME  =( (sum(sum(S))/(m*n)))^(1/2);
%峰值信噪比PSNR
PSNR = 10*log10(255^2/RSME);

%方差与不均匀度
for i = 1:m
        for j = 1:n
             STD1(i,j)= double((double(I(i,j))-ME1)^2);
        end
end
STD = (sum(sum(STD1))/(m*n))^(1/2);
DET1 = STD/ME1;

for i = 1:m
        for j = 1:n
             STD2(i,j)= double((double(J(i,j))-ME2)^2);
        end
end
STD3 = (sum(sum(STD2))/(m*n))^(1/2);
DET2 = STD3/ME2;

%质心位置
thersh_H1 = graythresh(I);
im_bw1 = im2bw(I,thersh_H1);
figure,imshow(im_bw1);
thersh_H2 = graythresh(J);
im_bw2 = im2bw(J,thersh_H2);
figure,imshow(im_bw2);
im_bw1 = bwareaopen(im_bw1,50);
im_bw2 = bwareaopen(im_bw2,50);
%二值化取反
im_bw1 = ~im_bw1;
im_bw2 = ~im_bw2;
%标注二进制图像中已连接的部分
[L,num]=bwlabel(im_bw1,8);     
[L1,num1]=bwlabel(im_bw2,8);     
%封装函数获取各种参数信息
stats_1 = regionprops(L,'Area','PixelList','Centroid','BoundingBox');
stats_2 = regionprops(L1,'Area','PixelList','Centroid','BoundingBox');
%绘制质心坐标
Cen_1 = cat(1,stats_1.Centroid);
Cen_2 = cat(1,stats_2.Centroid);
figure(8),imshow(im_bw1);
hold on ;
for i=1:length(stats_1) 
    plot(Cen_1(i,1), Cen_1(i,2), 'r+'); 
end
for i=1:length(stats_1) 
    plot(Cen_2(i,1), Cen_2(i,2), 'g+'); 
end

煤维纳滤波校正前后：

Snipaste_2024-04-14_20-57-21.png

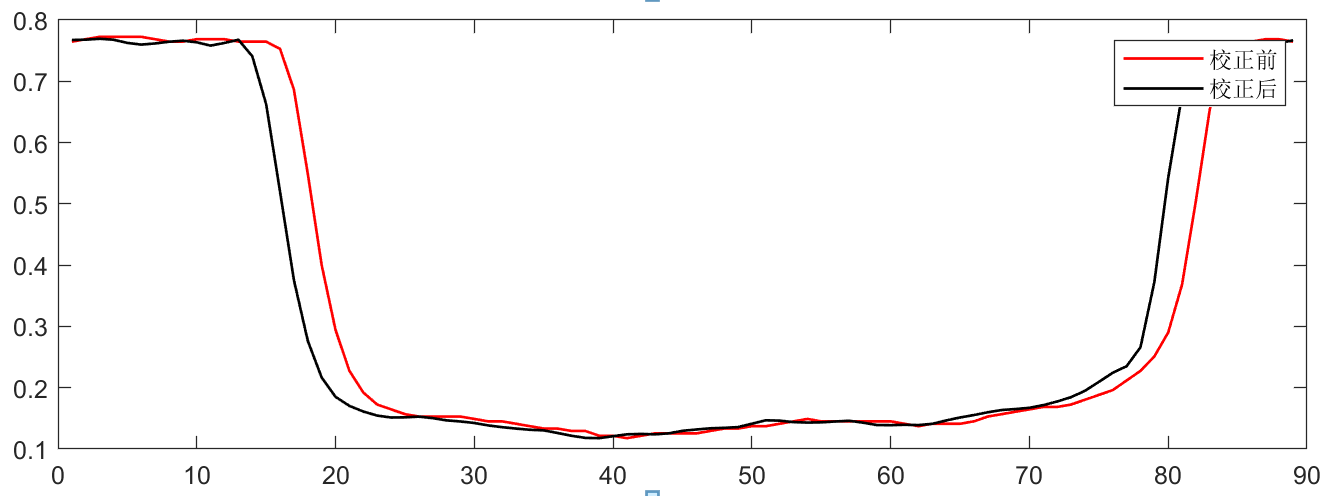
Snipaste_2024-04-14_20-58-09.png

滤波前后采用OTSU阈值分割形心位置变化：

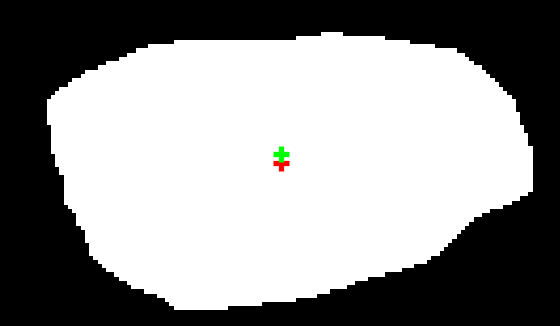
Snipaste_2024-04-14_21-00-14.png

Lucy-Richardson

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
clear all;
close all;
I = imread('C:\Users\雷子\Desktop\桌面文件\图像校正复原\余辉效应\1.bmp');
load PSF.mat;
W = fspecial('gaussian',[3,3],0.8);
I = imfilter(I , W, 'replicate');   
I = I(:,:,1);
I = im2double(I);
%Lucy-Richardson算法进行复原
PSF= PSF./ sum(PSF);
% NUMIT=20;
% J=deconvlucy(I,PSF',NUMIT);
NUMIT=20;
WT = ones(size(I));
% WT(5:end-4,5:end-4)=1;
V=0.1;
J=deconvlucy(I,PSF',NUMIT,sqrt(V),WT);
%
% J = J.*605;
figure;
subplot(121), imshow(I);
subplot(122), imshow(J);

plot(I(:,30),'r'), hold on;
plot(J(:,30),'k'), hold on;
%对校正进行修复
[m,n] = size(J);
for  i = 1:m
    for j = 1:n
        if J(i,j) >=0.8
            J(i,j) = 0.76;
        end
    end
end

for  i = 1:m
    for j = 1:n
        if J(i,j) <=0.02
           J(i,j) = 0.047;
        end
    end
end
%滤波处理
W = fspecial('gaussian',[3,3],0.8);
J= imfilter(J, W, 'replicate');   

figure;
subplot(121), imshow(I);
subplot(122), imshow(J);
plot(I(:,80),'r'), hold on;
plot(J(:,80),'k'), hold on;
%校正前后参数变化
%图像的灰度均值
ME1 = mean(mean(I));
ME2 = mean(mean(J));

%计算评价参数均方根误差RMSE
for i= 1:m
    for j = 1:n
        S(i,j) =double((J(i,j)-double(I(i,j)))^2);
    end
end
RSME  =( (sum(sum(S))/(m*n)))^(1/2);
%峰值信噪比PSNR
PSNR = 10*log10(255^2/RSME);

%方差与不均匀度
for i = 1:m
        for j = 1:n
             STD1(i,j)= double((double(I(i,j))-ME1)^2);
        end
end
STD = (sum(sum(STD1))/(m*n))^(1/2);
DET1 = STD/ME1;

for i = 1:m
        for j = 1:n
             STD2(i,j)= double((double(J(i,j))-ME2)^2);
        end
end
STD3 = (sum(sum(STD2))/(m*n))^(1/2);
DET2 = STD3/ME2;

%质心位置
thersh_H1 = graythresh(I);
im_bw1 = im2bw(I,thersh_H1);
figure,imshow(im_bw1);
thersh_H2 = graythresh(J);
im_bw2 = im2bw(J,thersh_H2);
figure,imshow(im_bw2);
%二值化取反
im_bw1 = ~im_bw1;
im_bw2 = ~im_bw2;
%标注二进制图像中已连接的部分
[L,num]=bwlabel(im_bw1,8);     
[L1,num1]=bwlabel(im_bw2,8);     
%封装函数获取各种参数信息
stats_1 = regionprops(L,'Area','PixelList','Centroid','BoundingBox');
stats_2 = regionprops(L1,'Area','PixelList','Centroid','BoundingBox');
%绘制质心坐标
Cen_1 = cat(1,stats_1.Centroid);
Cen_2 = cat(1,stats_2.Centroid);
figure(8),imshow(im_bw1);
hold on ;
for i=1:length(stats_1) 
    plot(Cen_1(i,1), Cen_1(i,2), 'r+'); 
end
for i=1:length(stats_1) 
    plot(Cen_2(i,1), Cen_2(i,2), 'g+'); 
end

煤LR滤波校正前后：

Snipaste_2024-04-15_16-06-49.png

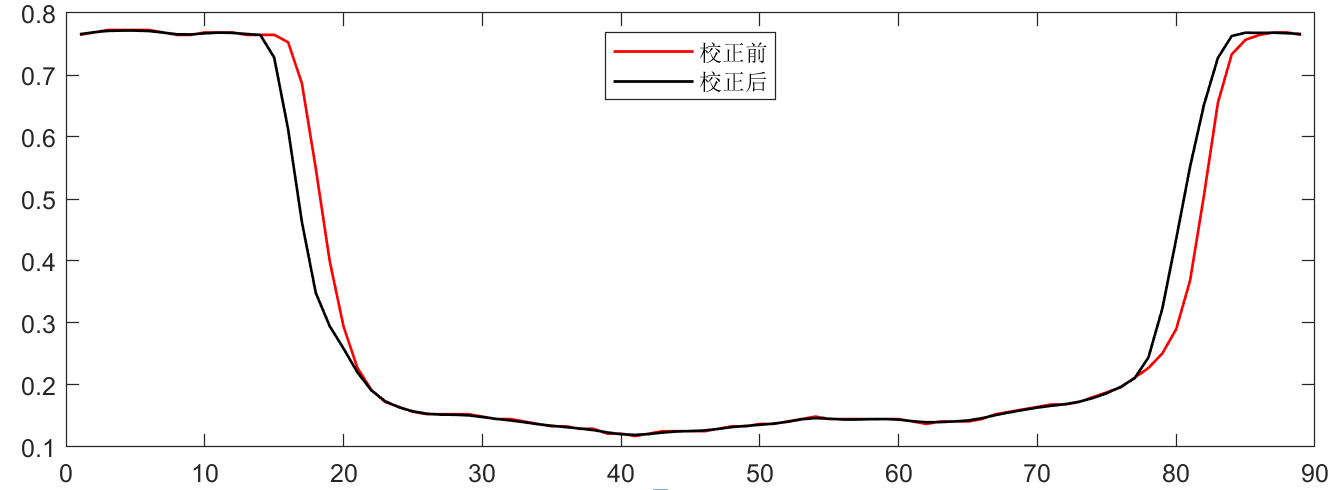
Snipaste_2024-04-15_16-07-34.png

滤波前后采用OTSU阈值分割形心位置变化：

Snipaste_2024-04-15_16-09-46.png

矸石LR滤波校正前后：

3.png

小粒径(<30 mm)矸石Lucy-Richardson复原结果：

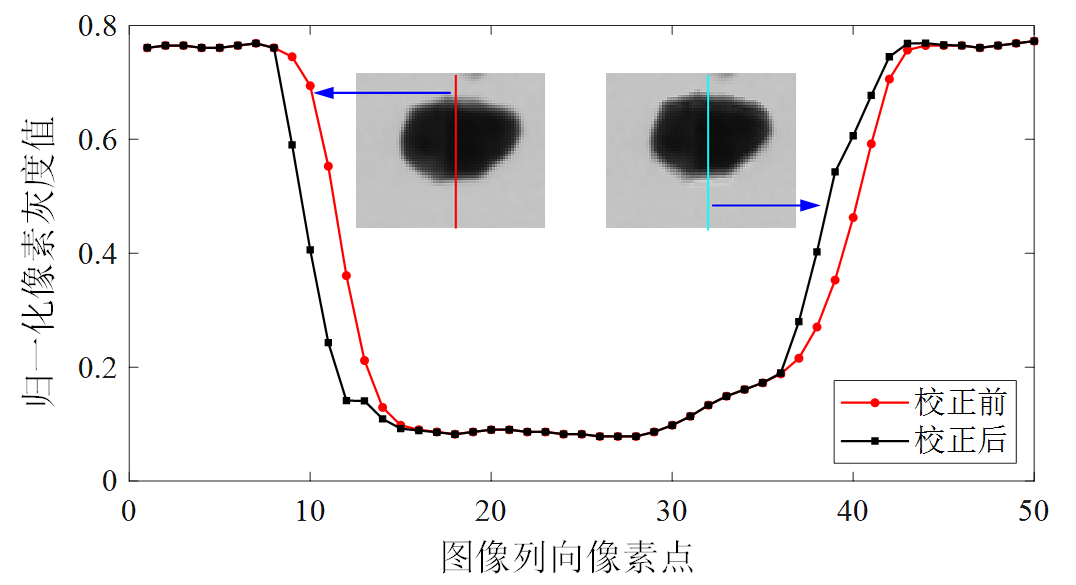
Snipaste_2024-04-15_16-13-46.png

小粒径(<30 mm)煤Lucy-Richardson复原结果：

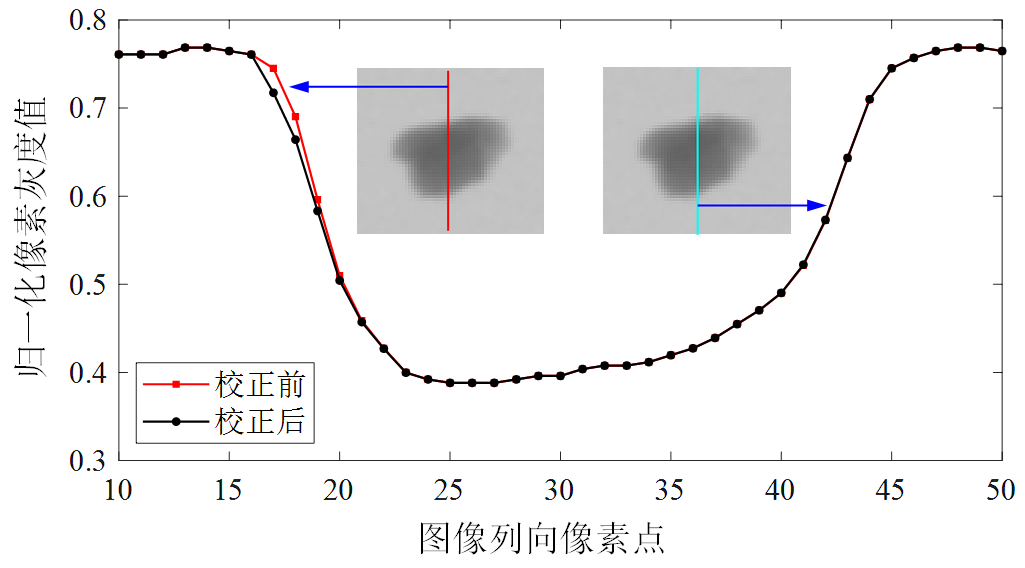
Snipaste_2024-04-15_16-13-52.png

约束最小二乘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
clear all;
close all;
I = imread('C:\Users\雷子\Desktop\桌面文件\图像校正复原\余辉效应\1.bmp');
load PSF.mat;
W = fspecial('gaussian',[3,3],0.8);
I = imfilter(I , W, 'replicate');   
I = I(:,:,1);
I = im2double(I);

PSF= PSF./ sum(PSF);
%约束最小二乘
NOISERPOWER=2;
J=deconvreg(I,PSF',NOISERPOWER);
%
% J = J.*605;
figure;
subplot(121), imshow(I);
subplot(122), imshow(J);

plot(I(:,80),'r'), hold on;
plot(J(:,80),'k'), hold on;
%对校正进行修复
[m,n] = size(J);
for  i = 1:m
    for j = 1:n
        if J(i,j) >=0.8
            J(i,j) = 0.76;
        end
    end
end

for  i = 1:m
    for j = 1:n
        if J(i,j) <=0.02
           J(i,j) = 0.047;
        end
    end
end
%滤波处理
W = fspecial('gaussian',[3,3],0.8);
J= imfilter(J, W, 'replicate');   

figure;
subplot(121), imshow(I);
subplot(122), imshow(J);
plot(I(:,80),'r'), hold on;
plot(J(:,80),'k'), hold on;

%图像的灰度均值
ME1 = mean(mean(I));
ME2 = mean(mean(J));

%计算评价参数均方根误差RMSE
for i= 1:m
    for j = 1:n
        S(i,j) =double((J(i,j)-double(I(i,j)))^2);
    end
end
RSME  =( (sum(sum(S))/(m*n)))^(1/2);
%峰值信噪比PSNR
PSNR = 10*log10(255^2/RSME);

%方差与不均匀度
for i = 1:m
        for j = 1:n
             STD1(i,j)= double((double(I(i,j))-ME1)^2);
        end
end
STD = (sum(sum(STD1))/(m*n))^(1/2);
DET1 = STD/ME1;

for i = 1:m
        for j = 1:n
             STD2(i,j)= double((double(J(i,j))-ME2)^2);
        end
end
STD3 = (sum(sum(STD2))/(m*n))^(1/2);
DET2 = STD3/ME2;

%质心位置
thersh_H1 = graythresh(I);
im_bw1 = im2bw(I,thersh_H1);
figure,imshow(im_bw1);
thersh_H2 = graythresh(J);
im_bw2 = im2bw(J,thersh_H2);
figure,imshow(im_bw2);
%二值化取反
im_bw1 = ~im_bw1;
im_bw2 = ~im_bw2;
%标注二进制图像中已连接的部分
[L,num]=bwlabel(im_bw1,8);     
[L1,num1]=bwlabel(im_bw2,8);     
%封装函数获取各种参数信息
stats_1 = regionprops(L,'Area','PixelList','Centroid','BoundingBox');
stats_2 = regionprops(L1,'Area','PixelList','Centroid','BoundingBox');
%绘制质心坐标
Cen_1 = cat(1,stats_1.Centroid);
Cen_2 = cat(1,stats_2.Centroid);
figure(8),imshow(im_bw1);
hold on ;
for i=1:length(stats_1) 
    plot(Cen_1(i,1), Cen_1(i,2), 'r+'); 
end
for i=1:length(stats_1) 
    plot(Cen_2(i,1), Cen_2(i,2), 'g+'); 
end

煤约束最小二乘滤波校正前后：

Snipaste_2024-04-15_18-19-07.png

Snipaste_2024-04-15_18-20-03.png

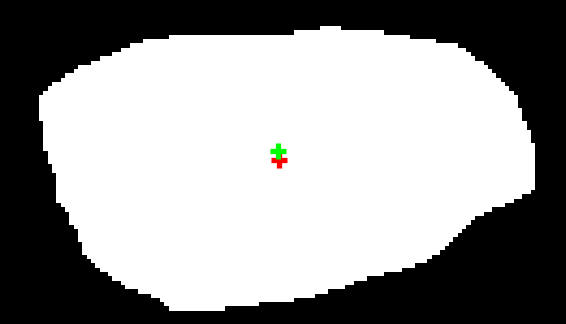
滤波前后采用OTSU阈值分割形心位置变化：

Snipaste_2024-04-15_18-22-02.png

从表 中复原结果来看维纳滤波复原后标准差变化较小，然而维纳滤波复原后图像平坦区域大量像素值发生变化。相比较于维纳滤波复原，采用Lucy-Richardson复原平坦区域像素值基本保持不变，因此认为Lucy-Richardson更能保障复原后的图像质量。但采用Lucy-Richardson复原对粒径低于30 mm的煤复原效果不理想，煤离开X射线透射后的成像边缘复原效果较差。约束最小二乘复原尽管复原前后标准差变化较小，但在噪声强度设定过大时引起边缘细节的丢失。

采用LR方法对多目标处理，滤波前后（右滤波后）：

Snipaste_2024-04-15_18-23-41.png

滤波前后采用分块OTSU阈值分割形心位置变化：

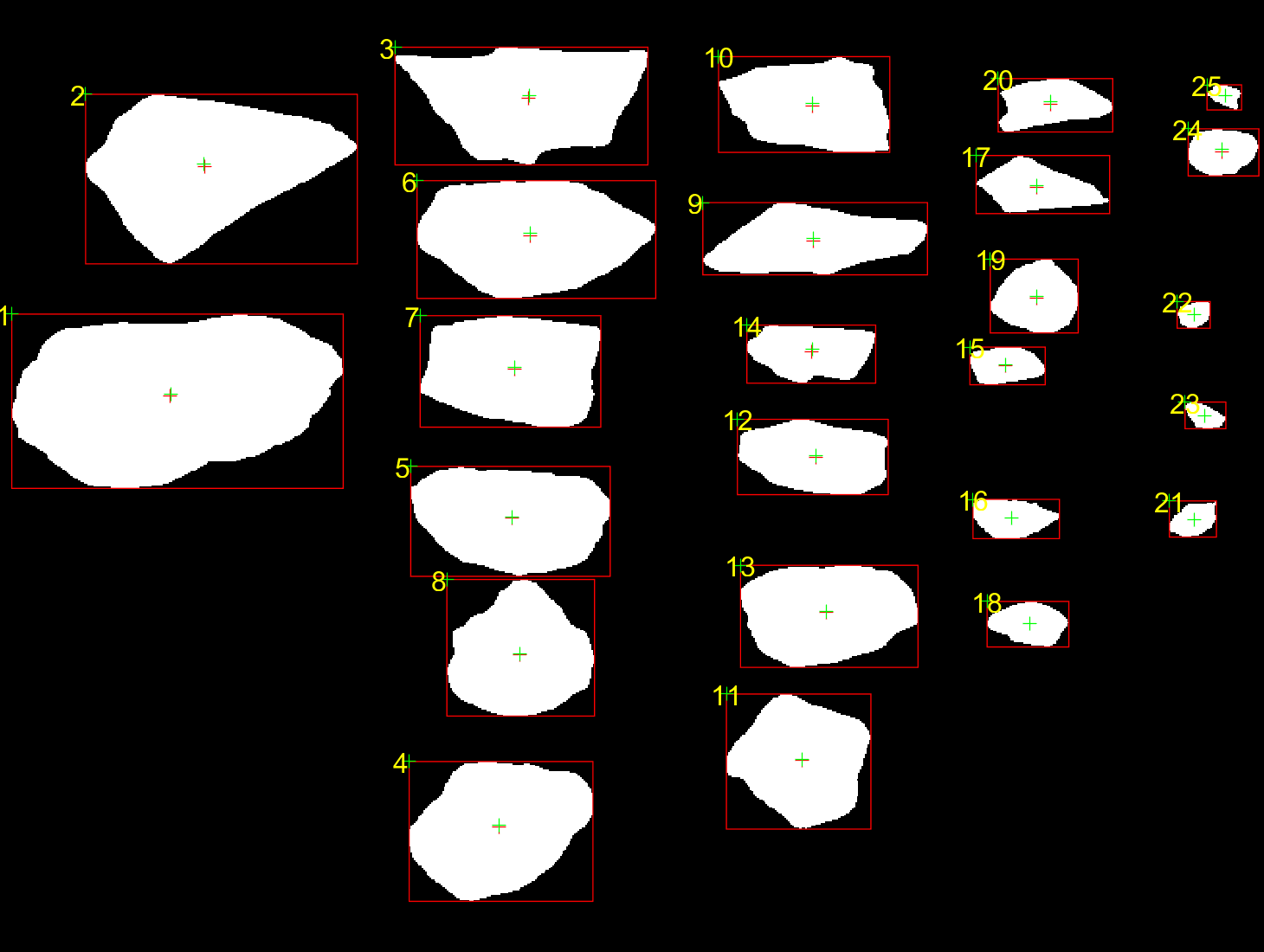
Snipaste_2024-04-15_18-30-53.png

采用余辉复原后图像的边缘像素值可迅速下降或提高，部分边缘像素值经余辉复原后变为背景值，原本接近于背景像素值的像素变为成像目标区域的像素。于是复原前后采用分块OTSU阈值分割会出现目标位置的偏移，在计算图像目标二值化区域形心时会出现偏差。上图 所示是采用LR复原前后计算的形心位置差异，绿色十字为复原后的形心。形心位置只在列向出现偏移，横向仍然保持不变或变化较小。

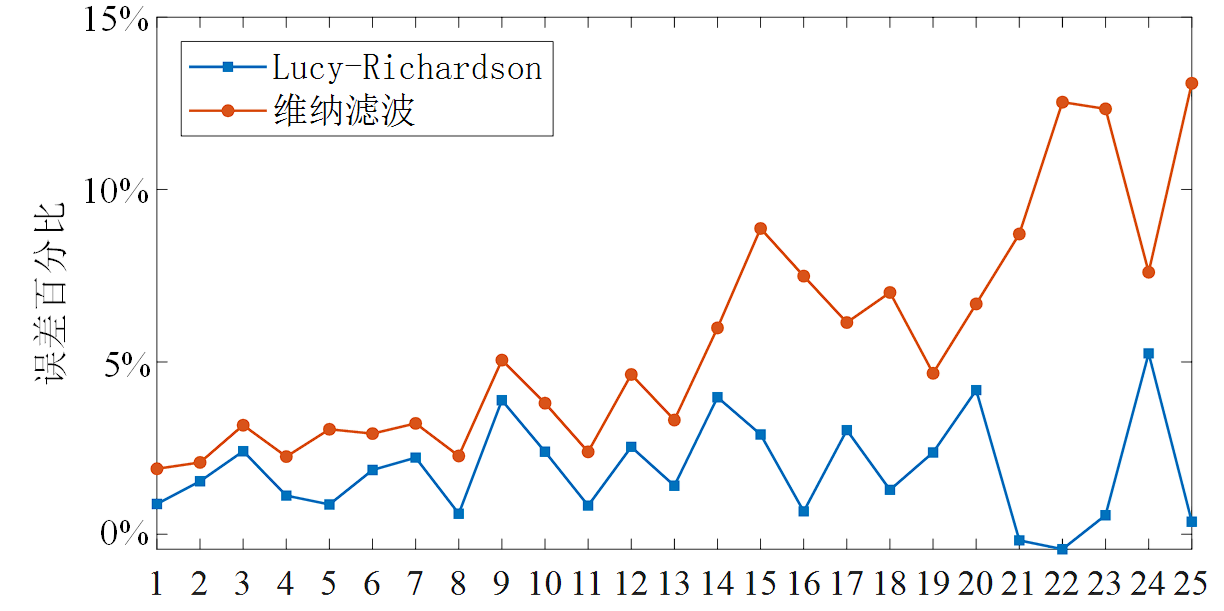
对比维纳滤波复原和Lucy-Richardson复原前后目标二值化区域形心位置差异。误差百分比表示复原后列向位置坐标变化量占原目标区域最小外接矩形的宽度百分比。维纳滤波复原后对形心位置造成的偏移量更大，而Lucy-Richardson复原由于对粒径较小的煤复原效果较差几乎不造成位置偏移，例如连通域21、22、23。采用Lucy-Richardson复原形心列向最大偏移量达到5.25%，平均偏移1.86%；维纳滤波复原形心列向最大偏移量达到13.08 %，平均偏移5.65%。由此可见，对于DE-XRT高速采集成像，必须进行余辉复原才能精准的计算目标实际形心位置，获取真实的目标二值化区域。尤其针对小粒径的煤矸，余辉复原后位置偏差较大，甚至会因定位精度较低造成无效吹射分离。

Snipaste_2024-04-15_18-27-26.png