分水岭算法理解与MATLAB实例分析

发表于 更新于 分类于 ， 阅读次数： 本文字数： 6.3k 阅读时长 ≈ 6 分钟

分水岭算法理解与MATLAB实例分析

​ 如下图所示：

Snipaste_2020-06-14_14-55-44.jpg

​ 苹果与苹果之间均有粘连，如果使用大津法做图像分割，则会将粘连的多个苹果分割为一个。

​ 分水岭算法将图像看作一个拓扑地形图，其中灰度值被认为是地形高度值。高灰度值对应着山峰，低灰度值对应着山谷。

​ 如下图所示（原图像）：

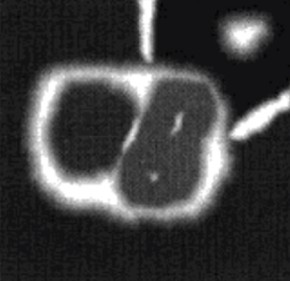
Snipaste_2020-06-14_14-53-08.jpg

​ 将原图像进行处理转化为地形俯视图：

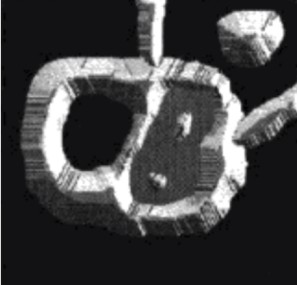
Snipaste_2020-06-14_14-54-20.jpg

​ 地形图三维视图：

Snipaste_2020-06-14_14-54-36.jpg

​ 将水从任一处留下来，它会朝地势较低的地方流动，直到某一局部低洼处才停下来。这个低洼处被称为吸水盆地。最终所有的水都会聚集在不同的吸水盆地。

​ 吸水盆地之间的山脊被称为分水岭。

​ 水从分水岭留下时，它朝不同吸水盆地流去的可能性相同。

- 最小值点：水最终汇集的地方；
- 盆地边缘点：水会等概率的流向任何盆地；
- 盆地其他点：水会聚集到局部最小点。

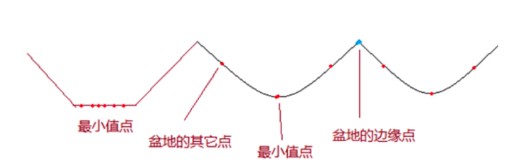
Snipaste_2020-06-14_15-00-50.jpg

​ 上图中红色的点可以视作注水口。

​ 假设我们在盆地的最小值点打一个洞，然后往盆地里面注水，并且阻止两个盆地的水汇集，并在两个盆地的水汇集的时刻，在交界线的边缘上（也即分水岭线），建立一个水坝，来阻止两个盆地的水汇集成一片水域。

​ 这样图像就被分成2个像素集，一个是注水盆地像素集，一个是分水岭线像素集。

​ 对应到图像分割，就是要在灰度图像中找到不同的吸水盆地和分水岭。

​ 不同的吸水盆地和分水岭组成的区域即为我们要分割的目标。

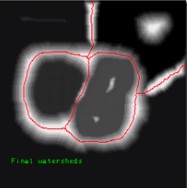
Snipaste_2020-06-14_15-07-59.jpg

​ 逐渐漫水过程示意图：

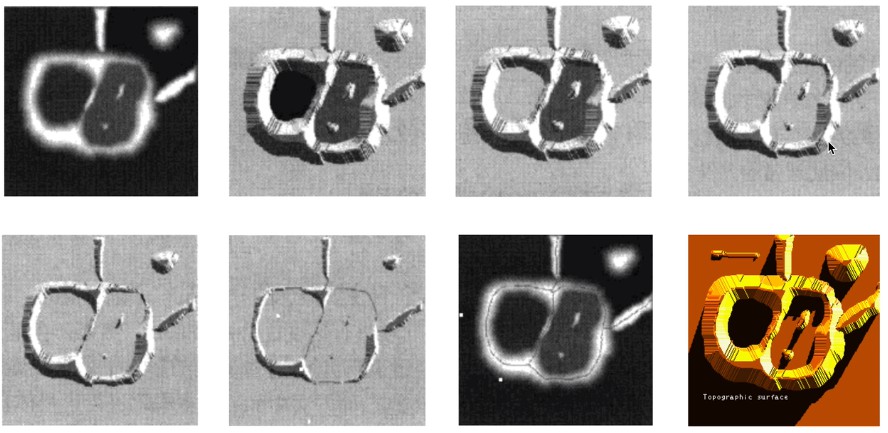
Snipaste_2020-06-14_15-10-06.jpg

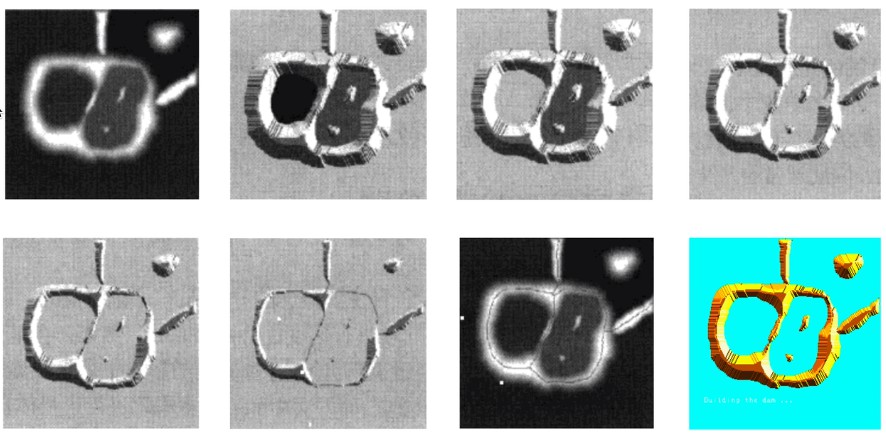
Snipaste_2020-06-14_15-10-22.jpg

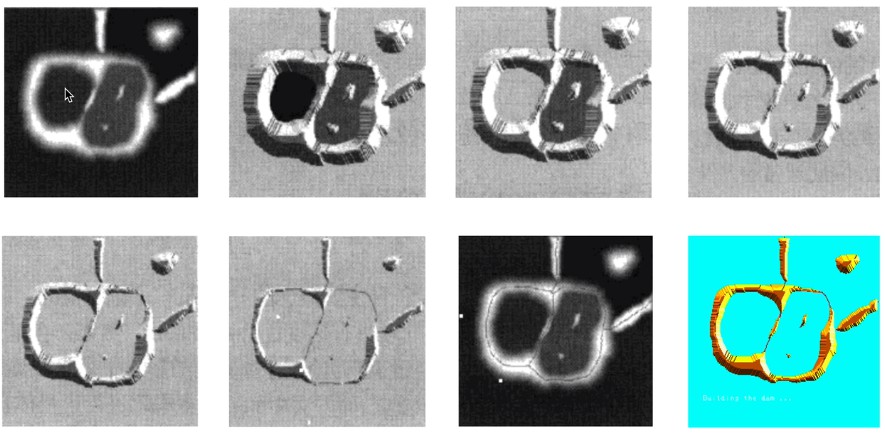
Snipaste_2020-06-14_15-10-36.jpg

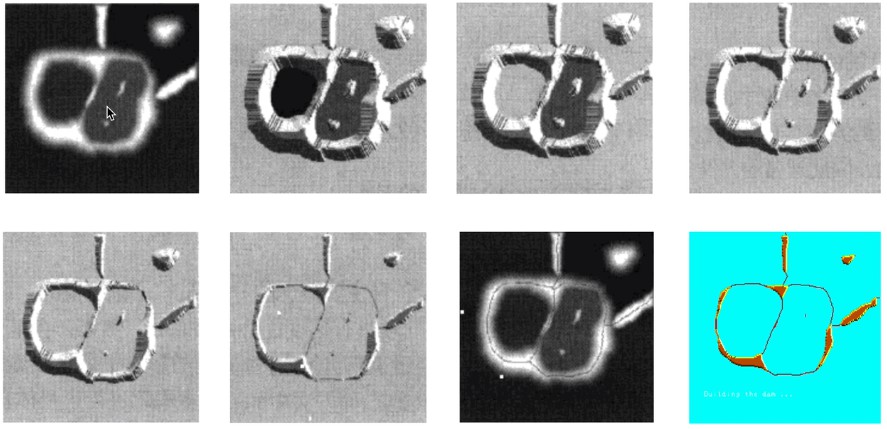
Snipaste_2020-06-14_15-10-55.jpg

​ 最终我们想要的结果：

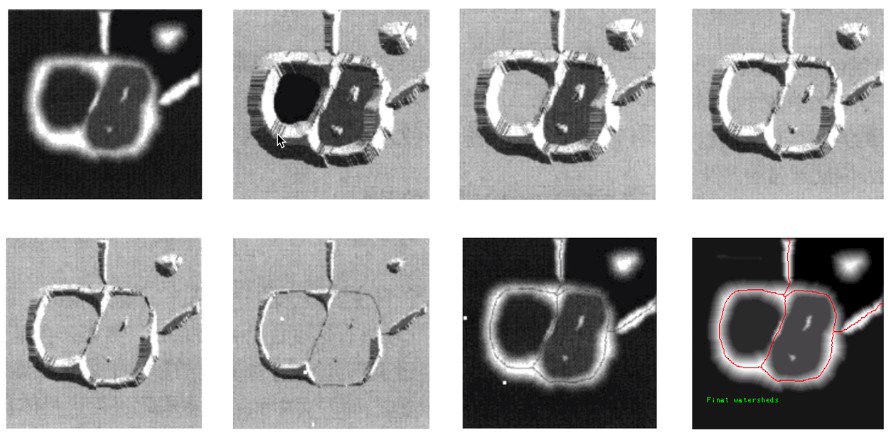
Snipaste_2020-06-14_15-11-15.jpg

水坝的构建

  • 在实际操作中，水位的上升常利用灰度0~255的分层处理来实现，当处理到第N层时，灰度小于N的像素就会被淹没。
  • 图中a显示了两个相邻聚水盆，其中颜色越深的区域海拔越低。
  • 当水位逐渐上升到第N-1阶段时，黑色区域首先被淹没。
  • 借助膨胀的方法，在水域之间适当的位置构建堤坝防止水域的连通。

Snipaste_2020-06-14_15-16-06.jpg

Snipaste_2020-06-14_15-18-50.jpg

分水岭算法实现步骤：

Snipaste_2020-06-14_15-19-56.jpg

分水岭算法的实现

​ 在MATLAB中，函数watershed（）即为分水岭函数。L = watershed（A），L是一个标记矩阵，标记分水岭算法分割出的各“分水岭”区域。

Snipaste_2020-06-14_15-22-11.jpg

1
2
3
4
rgb = imread('pears.png');
I = rgb2gray(rgb);
subplot(121),imshow(rgb);
subplot(122),imshow(I);

Snipaste_2020-06-14_15-28-13.jpg

​ 为了更加突出边缘信息，针对梯度图像进行处理：

1
2
3
4
5
6
%求灰度图像梯度图像
hy = fspecial('sobel');hx = hy';    %sobel水平边缘增强滤波器，用于边缘提取
Iy = imfilter(double(I),hy,'replicate');    %Iy方向梯度分量
Ix = imfilter(double(I),hx,'replicate');    %Ix方向梯度分量
gradmag = sqrt(Ix.^2 + Iy.^2);
figure(2),imshow(gradmag,[]),title('梯度幅值图像');

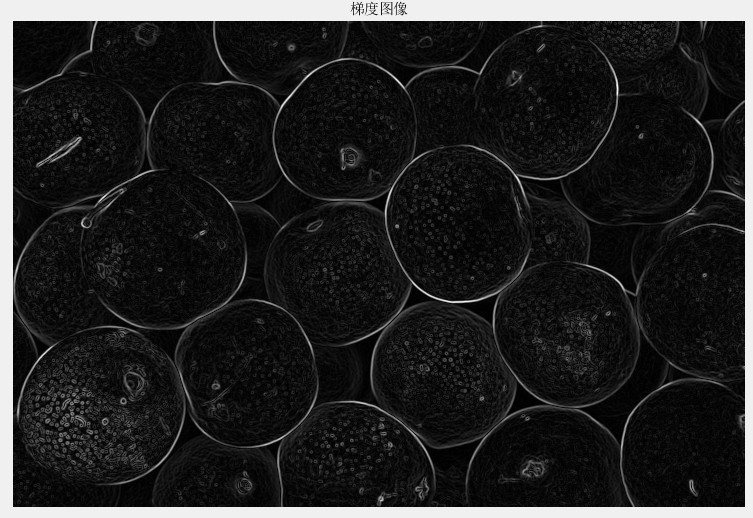
Snipaste_2020-06-14_15-38-54.jpg

​ 接下来使用梯度幅值图像做分水岭：

1
2
3
4
%使用分水岭函数分割图像
L = watershed(gradmag);
Lrgb = label2rgb(L);
figure(3),imshow(Lrgb),title('梯度幅值图像做分水岭');

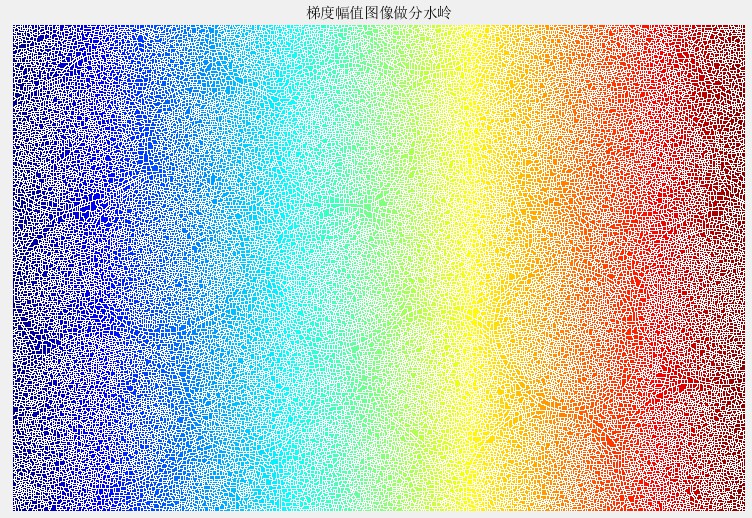
Snipaste_2020-06-14_15-43-53.jpg

​ 结果图像过分割太严重（寻找到的局部极小值太多），接下来需要对其进行改进，首先标注，然后分割，即把较多的极小值点进行合并。

​ 事前标记(Mark)目标部分区域（运用形态学中的开闭运算），在这个区域的水淹没过程中，水平面都是从定义的高度开始的，这样可以避免一些很小的噪声极值区域的分割。

Snipaste_2020-06-14_15-52-56.jpg

1
2
3
4
5
6
7
8
%%
%标记前景对象
%基于开的重建和基于闭的重建来清理图像，在每个目标内创建单位极大值
se = strel('disk', 20);
Io = imopen(I, se); %图像开运算
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(I, []); title('灰度图像');
subplot(1, 2, 2); imshow(Io), title('图像开操作')

Snipaste_2020-06-14_22-48-36.jpg

1
2
3
4
5
6
%%
Ie = imerode(I, se); %腐蚀图像
Iobr = imreconstruct(Ie, I);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(I, []); title('灰度图像');
subplot(1, 2, 2); imshow(Iobr, []), title('基于开的重建图像')

Snipaste_2020-06-14_22-49-03.jpg

1
2
3
4
5
6
7
8
%%
Ioc = imclose(Io, se); %图像闭运算
Ic = imclose(I, se);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(I, []); title('灰度图像');
subplot(2, 2, 2); imshow(Io, []); title('开操作图像');
subplot(2, 2, 3); imshow(Ic, []); title('闭操作图像');
subplot(2, 2, 4); imshow(Ioc, []), title('开闭操作');

Snipaste_2020-06-14_22-55-20.jpg

1
2
3
4
5
6
7
8
9
%%
Iobrd = imdilate(Iobr, se);
Iobrcbr = imreconstruct(imcomplement(Iobrd), imcomplement(Iobr)); %对输出图像
Iobrcbr = imcomplement(Iobrcbr); %计算图像补集
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(I, []); title('灰度图像');
subplot(2, 2, 2); imshow(Ioc, []); title('开闭操作');
subplot(2, 2, 3); imshow(Iobr, []); title('基于开的重建图像');
subplot(2, 2, 4); imshow(Iobrcbr, []), title('基于闭的重建图像');

Snipaste_2020-06-14_22-55-54.jpg

1
2
3
4
5
6
%%
fgm = imregionalmax(Iobrcbr); %求取目标局部最大值区域
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 3, 1); imshow(I, []); title('灰度图像');
subplot(1, 3, 2); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(1, 3, 3); imshow(fgm, []); title('局部极大图像');

Snipaste_2020-06-14_22-57-51.jpg

1
2
3
4
5
6
7
8
9
%%
%叠加前景标记到原图
It1 = rgb(:, :, 1);
It2 = rgb(:, :, 2);
It3 = rgb(:, :, 3);
It1(fgm) = 255; It2(fgm) = 0; It3(fgm) = 0;
I2 = cat(3, It1, It2, It3); %前景填充为红色
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(rgb, []); title('原图像');

Snipaste_2020-06-14_22-58-28.jpg

1
2
3
4
5
6
7
8
9
10
 %%
%清理标记斑点边缘
se2 = strel(ones(5,5));
fgm2 = imclose(fgm, se2); %闭运算
fgm3 = imerode(fgm2, se2); %图像腐蚀
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(2, 2, 2); imshow(fgm, []); title('局部极大图像');
subplot(2, 2, 3); imshow(fgm2, []); title('闭操作');
subplot(2, 2, 4); imshow(fgm3, []); title('腐蚀操作');

Snipaste_2020-06-14_23-02-31.jpg

1
2
3
4
5
6
7
8
9
10
11
12
%%
fgm4 = bwareaopen(fgm3, 20); %移除小面积连通块
It1 = rgb(:, :, 1);
It2 = rgb(:, :, 2);
It3 = rgb(:, :, 3);
It1(fgm4) = 255; It2(fgm4) = 0; It3(fgm4) = 0;
I3 = cat(3, It1, It2, It3);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(I2, []); title('局部极大叠加到原图像');
subplot(2, 2, 2); imshow(fgm3, []); title('闭腐蚀操作');
subplot(2, 2, 3); imshow(fgm4, []); title('去除小斑点操作');
subplot(2, 2, 4); imshow(I3, []); title('修改局部极大叠加到原图像');

Snipaste_2020-06-14_23-16-25.jpg

1
2
3
4
5
6
 %%
%大津法计算背景标记
bw = im2bw(Iobrcbr, graythresh(Iobrcbr));
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(1, 2, 2); imshow(bw, []); title('阈值分割');

Snipaste_2020-06-14_23-03-15.jpg

1
2
3
4
5
6
7
8
9
%%
D = bwdist(bw); %计算二值图像欧几里得矩阵
DL = watershed(D); %分水岭
bgm = DL == 0; %寻找分水岭脊线
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(2, 2, 2); imshow(bw, []); title('阈值分割');
subplot(2, 2, 3); imshow(label2rgb(DL), []); title('分水岭变换示意图');
subplot(2, 2, 4); imshow(bgm, []); title('分水岭变换脊线图');

Snipaste_2020-06-14_23-05-34.jpg

1
2
3
4
5
6
7
%%
gradmag2 = imimposemin(gradmag, bgm | fgm4); %修改图像使其只在特定的要求位置有局部
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(bgm, []); title('分水岭变换脊线图');
subplot(2, 2, 2); imshow(fgm4, []); title('前景标记');
subplot(2, 2, 3); imshow(gradmag, []); title('梯度幅值图像');
subplot(2, 2, 4); imshow(gradmag2, []); title('修改梯度幅值图像');

Snipaste_2020-06-14_23-20-50.jpg

1
2
3
4
5
6
7
8
9
10
11
12
%%
%可视化
It1 = rgb(:, :, 1);
It2 = rgb(:, :, 2);
It3 = rgb(:, :, 3);
L = watershed(gradmag2);
fgm5 = imdilate(L == 0, ones(3, 3)) | bgm | fgm4;
It1(fgm5) = 255; It2(fgm5) = 0; It3(fgm5) = 0;
I4 = cat(3, It1, It2, It3);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(rgb, []); title('原图像');
subplot(1, 2, 2); imshow(I4, []); title('标记和对象边缘叠加到原图像');

Snipaste_2020-06-14_23-22-30.jpg

1
2
3
4
5
6
7
8
9
10
11
12
13
%%
%可视化
Lrgb = label2rgb(L, 'jet', 'w', 'shuffle'); %转换为伪彩色图像
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(rgb, []); title('原图像');
subplot(1, 2, 2); imshow(Lrgb); title('彩色分水岭标记矩阵');
%%
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(rgb, []); title('原图像');
subplot(1, 2, 2); imshow(rgb, []); hold on;
himage = imshow(Lrgb);
set(himage, 'AlphaData', 0.3);
title('标记矩阵叠加到原图像');

Snipaste_2020-06-14_23-23-42.jpg

Snipaste_2020-06-14_23-23-52.jpg

​ 使用分水岭算法应对图像目标区域沾连分割问题，常能达到意象不到的效果。

内容参考：